加快计算速度揭示电子在材料中的相互作用

材料科学家和工程师希望准确了解电子在新材料中如何相互作用和移动，以及用这些材料制成的设备将如何工作。电流在材料内是否能顺利流动?材料在某个温度下会变成超导，使电流无需电源即可流动?电子自旋的量子态在新的电子和量子设备中能保持多长时间?

材料物理学家团体试图通过了解材料内部发生的情况、计算其行为直至单个电子相互作用和原子运动的水平来解决这些问题。

现在，加州理工学院的一个研究小组取得了一项重要发现，有助于简化此类计算，在保持准确性的同时将其速度提高 50 倍或更多。因此，可以计算更复杂材料和设备中的电子相互作用，并开发以前认为不可能的新计算。

在《物理评论 X》杂志上发表的一篇新论文中，加州理工学院应用物理学研究生姚罗、他的导师、应用物理学、物理学和材料科学教授马可·贝尔纳迪和同事描述了一种实现这些进步的新数据驱动方法。他们的方法简化了用于表示材料中电子与原子振动(或声子，可视为振动能量的单个单位)之间相互作用的密集计算矩阵。

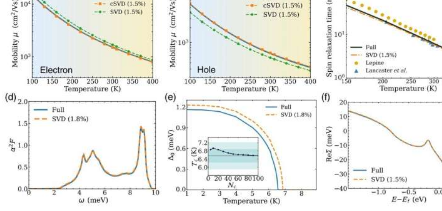
罗和伯纳迪表示，新方法使他们仅使用通常用于解决此类问题的 1% 到 2% 的数据，大大加快了计算速度，并在此过程中揭示了决定材料特性的最重要的相互作用。

“这非常令人惊讶，”Bernardi 说。“用压缩矩阵计算的电子-声子相互作用几乎与完整计算一样准确。这极大地减少了计算时间和内存使用量，在大多数情况下大约减少了两个数量级。这也是奥卡姆剃刀的一个优雅例子，即倾向于使用参数数量最少的简单物理模型。”

为该领域寻找新的中间立场

该领域的研究人员通常采用两种方法之一来从最基本的层面理解材料。一种方法强调建立最小模型，降低系统的复杂性，以便研究人员可以通过纸笔计算调整一些参数来定性地了解材料。

另一种方法从材料的结构开始，使用所谓的“第一原理”方法(需要大型计算机的量子力学计算)来定量精确地研究材料特性。

后一种方法是 Bernardi 团队重点研究的，它使用包含数十亿个条目的超大矩阵来计算控制各种物理特性的电子相互作用。这意味着每次计算都要花费数千小时的计算时间。Bernardi 表示，这项新研究提出了一种介于这两种方法之间的中间立场。

“通过我们的新方法，您可以截断这些矩阵的大小，提取关键信息，并生成材料中相互作用的最小模型。”

找出最重要的奇异值

他的团队采用的方法是基于将一种称为奇异值分解 (SVD) 的方法应用于材料中的电子-声子相互作用。SVD 技术广泛应用于图像压缩和量子信息科学等领域。在这里，它允许作者分离或解开数千或数百万个电子-声子相互作用矩阵中的电子和振动成分，并为每个基本相互作用分配一个数字。

这些实数正数称为奇异值，它们按重要性对基本相互作用进行排序。然后，程序可以消除每个矩阵中除几个百分点以外的所有相互作用，只留下主要的奇异值，这一过程使确定成本降低，其成本与压缩量成正比。

因此，例如，如果程序仅保留 1% 的奇异值，则计算速度将提高 100 倍。研究人员发现，仅保留一小部分奇异值(通常为 1% 到 2%)，近似结果的精度几乎与完整计算相同。

“通过使用 SVD，你可以减少奇异值的数量，并仅捕捉表示给定材料中电子相互作用的矩阵的主要特征，”该论文的第一作者、Bernardi 团队的三年级学生 Luo 说道。

“这会截断原始矩阵，从而加快算法速度，并且还有揭示材料中哪些相互作用占主导地位的额外好处。”

Bernardi 指出，SVD 方法的后一个优点使研究人员能够“直观地了解材料中的电子相互作用，这是过去第一原理计算中所缺少的。例如，在涉及硅的计算中，很明显，主要的奇异值与特定键的拉伸和压缩有关。

“这很简单，但在进行计算之前，我们并不知道这是最强的相互作用，”伯纳迪解释道。

在论文中，研究人员表明，使用 SVD 方法压缩与电子-声子相互作用相关的矩阵，可以为研究人员可能想要计算的材料的各种特性提供准确的结果，包括电荷传输、自旋弛豫时间和超导体的转变温度。

Bernardi 和他的团队正在将基于 SVD 的计算扩展到材料中更广泛的相互作用，并开发以前被认为不可能的高级计算。该团队还致力于将新的 SVD 方法添加到其开源 Perturbo 代码中，这是一个帮助研究人员计算电子在材料中如何相互作用和移动的软件包。Bernardi 表示，这将使科学界的用户能够更快地预测与电子-声子相互作用相关的材料特性。

这篇论文的标题是“数据驱动的电子-声子相互作用压缩”。除了 Luo 和 Bernardi 之外，这篇论文的合著者还包括研究生 Dhruv Desai (MS '22)、Benjamin Chang (MS '20) 和 Jinsoo Park (Ph.D. '22)，后者现在是芝加哥大学的博士后研究员。

　　免责声明：本文由用户上传，与本网站立场无关。财经信息仅供读者参考，并不构成投资建议。投资者据此操作，风险自担。 如有侵权请联系删除！